시계열에서 튀는 곳 찾기
이상 탐지
시계열 데이터를 가지고 할 만한 건 이상 탐지와 예측이다. 이상 탐지에서는 “이상(abnormal)”이 뭐냐에 따라 적당한 방법이 다르다. 예를 들어 냉장고 온도 데이터에서 이상을 탐지할 때라면 값이 어떤 정상 범위 안에 있는지 보면 된다. 기존에 모아 둔 데이터가 있다면 정상 범위를 알아서 추측할 수도 있을 거다. 체온 데이터에도 같은 방식을 쓸 수 있겠지만, 한발 더 나아가 기존 데이터에서 일, 월, 년 등에 따른 주기적 변동성(seasonality)을 뽑아낼 수 있다. 그러면 값을 예측하는 게 가능해지고, 측정치가 예측치와 많이 다를 때 이상이라고 판단하면 된다. 더불어 가령 지구 평균 기온 데이터라면 추세(trend) 요소까지 도입하면 된다.
직간접적으로 물리적 운동을 측정한 데이터에는 주기성이 있을 때가 많다. 변화가 없거나 발산만 하는 지표를 굳이 측정할 이유는 없을 테고, 운동원과 음성 피드백으로 이뤄진 시스템은 진동을 하기 마련이다. 공기가 진동하고, 기계가 진동하고, 심장이 진동한다.
이상 패턴이란 뭘까? 범용적으로 말하자면 “낮은 빈도로 등장하는 패턴”이다. 기존 자료에 등장한 여러 패턴들의 빈도를 계산해 둔 다음, 드물게 등장했던 패턴이나 본 적 없는 패턴을 만나면 이상 패턴이라고 하면 된다. 그러자면 기존 패턴들을 비슷한 것끼리 분류할 수 있어야 한다.
시나리오
공기가 진동하는 게 소리고, 귀는 튀는 소리를 잘 감지한다. 그렇다면 한번 흉내를 내 볼 만하다.
귓속에는 공명 진동수가 제각각인 털 달린 세포들이 있어서 진동수별로 진폭을 감지한다. 이걸 흉내낼 수 있는 게 푸리에 변환이고, 그래서 전통적인 음성 인식 알고리듬에도 푸리에 변환이 쓰인다.
일정 구간의 진동 데이터에 푸리에 변환을 적용하면 n차원 벡터가 (길이 n인 1차원 배열이) 나온다. 따라서 k-평균 알고리듬 등을 써서 분류를 할 수 있다.
“도레미파솔” 소리를 기준으로 어느 노래를 분류해 보자. 말하자면 다섯 가지 정해진 동작 속도가 있는 기계가 잘 돌고 있는지 확인하는 거다. 깔끔한 합성 데이터니까 필터링과 인터폴레이션은 필요치 않다.
준비
import librosa
import numpy as np
import matplotlib.pyplot as plt
y, sr = librosa.load('ts-doremi.mp3')
plt.plot(y[500:1000])
plt.show()
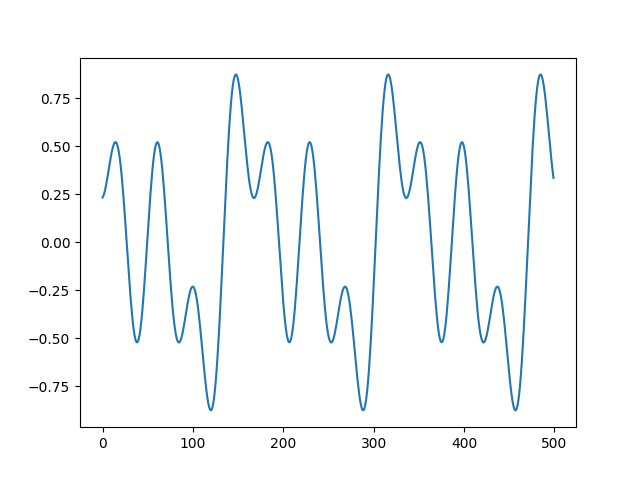
이 ‘측정치’에서 주파수 성분을 뽑아내 보자. 진폭이 아니라 진동수를 관찰하고 싶은 거니까 진폭을 정규화 하자.
doremi = np.abs(librosa.stft(y))
doremi /= np.clip(np.amax(doremi, axis=0), 0.1 * np.max(doremi), None)
doremi_t = np.transpose(doremi)
plt.plot(doremi_t)
plt.show()
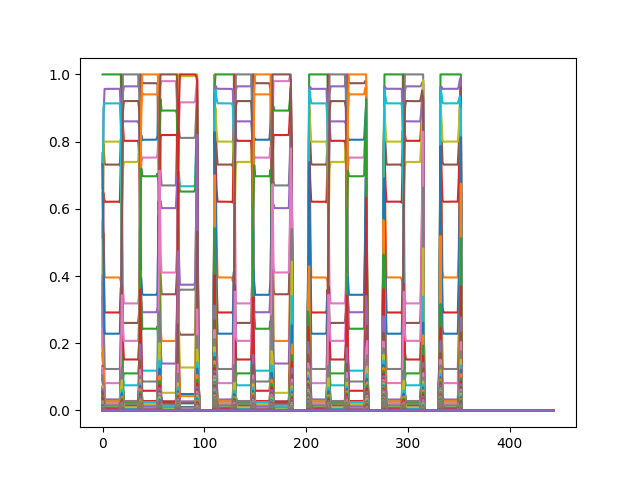
합성한 소리라 그런지 아주 깔끔하게 나온다. 좀 다르게도 보자.
plt.imshow(doremi[:150], origin='lower')
plt.show()
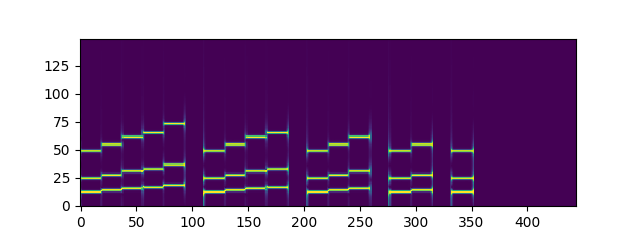
도-레-미-파-솔-쉬고. 경계에 있는 프레임의 흐릿한 값이 눈에 띈다.
K-means
업계 표준 방식을 써 보자. 깔끔하지 않은 값들이 있으니까 클러스터 수에 여유를 두자. 그리고 각 주파수 성분 크기가 다른 성분과 독립적인 게 아니니까 whitening은 하지 말자.
from scipy.cluster.vq import kmeans2
centroid, label = kmeans2(doremi_t, 15, iter=42, minit='points')
def sort_by_freq(centroid, label):
y_max = max(label)
# list of (original index, index after sort, occurrence)
sorter = [[i, 0, np.count_nonzero(label == i)] for i in range(y_max+1)]
sorter = sorted(sorter, key=lambda s: s[2], reverse=True)
sorted_centroid = [centroid[sorter[i][0]] for i in range(len(centroid))]
sorter = [(c[0], i, c[2]) for i, c in enumerate(sorter)]
sorter = sorted(sorter, key=lambda s: s[0])
sorted_label = [sorter[l][1] for l in label]
return (sorted_centroid, sorted_label)
centroid, label = sort_by_freq(centroid, label)
data = label[:220]
plt.scatter([x for x in range(len(data))], data)
plt.xticks([x for x in range(0, len(data), 37)])
plt.yticks(range(0, max(data)+1))
plt.grid()
plt.show()
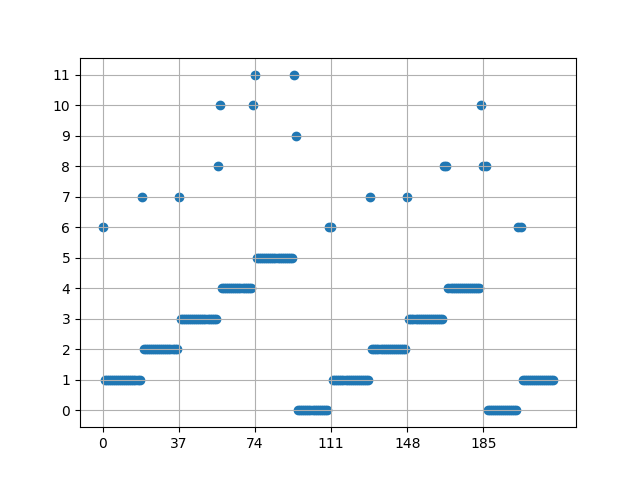
(k-평균은 지역 최적에 갇힐 수 있는 알고리듬이기에 실행마다 결과가 다를 수 있다.)
0에서 5까지를 정상 값으로 보면 될 것 같다. 0은 무음 구간이다. 중심과의 거리도 계산해 보자.
max_label = 5
doremi_dist = [np.linalg.norm(p - centroid[label[i]]) if label[i] <= max_label else None for i, p in enumerate(doremi_t)]
plt.plot(doremi_dist)
plt.show()
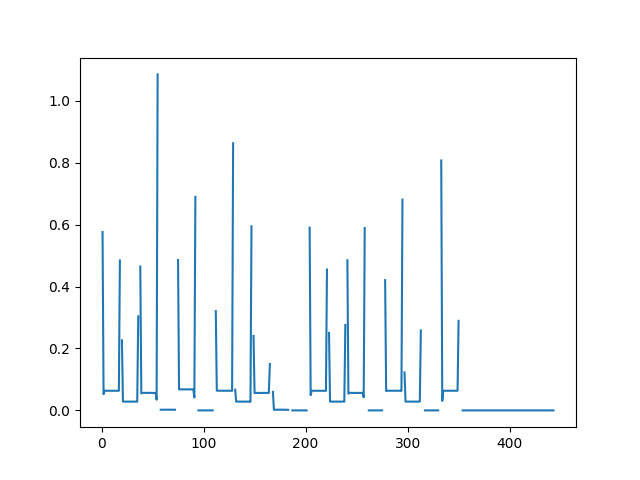
넉넉잡아 거리가 0.5를 계속 넘으면 이상하다고 보면 될 거 같다.
한 프레임만큼 데이터를 모은 다음 다음처럼 하면 된다.
- 푸리에 변환을 수행한다.
- 정규화를 수행한다.
- 가장 가까운 중심점을 찾는다.
- 그 중심과의 거리가 기준을 넘으면 비정상으로 판단한다.
y, sr = librosa.load('ts-shark.mp3')
shark = np.abs(librosa.stft(y))
shark /= np.clip(np.amax(shark, axis=0), 0.1 * np.max(shark), None)
shark_t = np.transpose(shark)
def to_cluster(p):
dist = map(lambda c: np.linalg.norm(p - c), centroid)
return min(enumerate(dist), key=lambda e: e[1])
print('Label: %d, Distance: %f' % to_cluster(shark_t[100]))
전체적으로 결과를 보자.
dist_limit = 0.5
shark_result = list(map(to_cluster, shark_t))
shark_label = list(map(lambda e: e[0], shark_result))
shark_dist = list(map(lambda e: e[1], shark_result))
fig, (ax1, ax2) = plt.subplots(nrows=2)
ax1.scatter([x for x in range(len(shark_label))], shark_label)
ax1.xticks([x for x in range(0, len(shark_label), 20)])
ax1.yticks(range(0, max(shark_label)+1))
ax1.grid()
ax1.axhline(max_label+.5, color='red', alpha=0.5, dashes=(4, 4))
ax2.plot(shark_dist)
ax2.axhline(dist_limit, color='red', alpha=0.5, dashes=(4, 4))
plt.show()
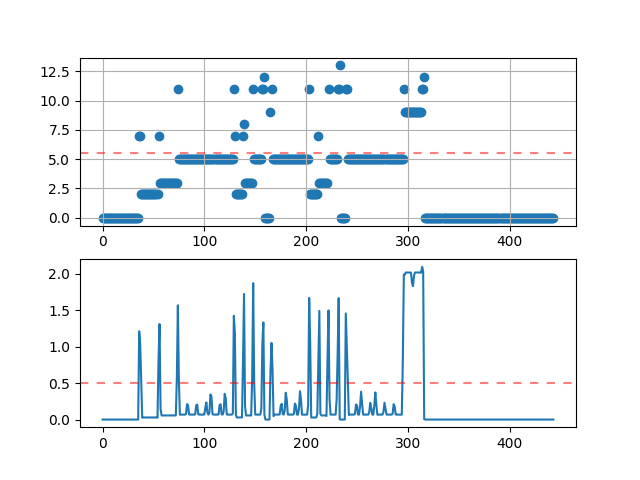
300번째 프레임 근처에 기준치를 계속 초과하는 구간이 눈에 띈다. 왜 그럴까?

역시나, 파 음에 샵이 있었다. 불현듯 떠오르는 파도솔레라미시…
요컨데 k-평균 알고리듬으로 꽤 깔끔하게 탐지가 된다.
ANN
k-평균 알고리듬으로 끝내기에는 좀 아쉽다. 괜시리 신경망을 써 보자. 마침 참고할 글도 있다.
입력 데이터가 길이 1025짜리 1차원 배열이니까 MNIST 데이터셋이랑 비슷한 수준이다. 간단한 망으로 충분하다.
import keras
data_size = len(doremi_t[0])
input_layer = keras.layers.Input(shape=(data_size,))
encoded = keras.layers.Dense(15, activation='sigmoid')(input_layer)
decoded = keras.layers.Dense(data_size)(encoded)
autoencoder = keras.models.Model(input_layer, decoded)
autoencoder.compile(optimizer='rmsprop', loss='mean_squared_error')
autoencoder.fit(doremi_t, doremi_t, epochs=500, batch_size=100,
shuffle=True, verbose=0,
validation_data=(doremi_t, doremi_t))
shark_pred = autoencoder.predict(shark_t)
shark_ann_dist = [float(np.linalg.norm(shark_t[i] - shark_pred[i])) for i in range(len(shark_t))]
plt.plot(shark_ann_dist)
plt.show()
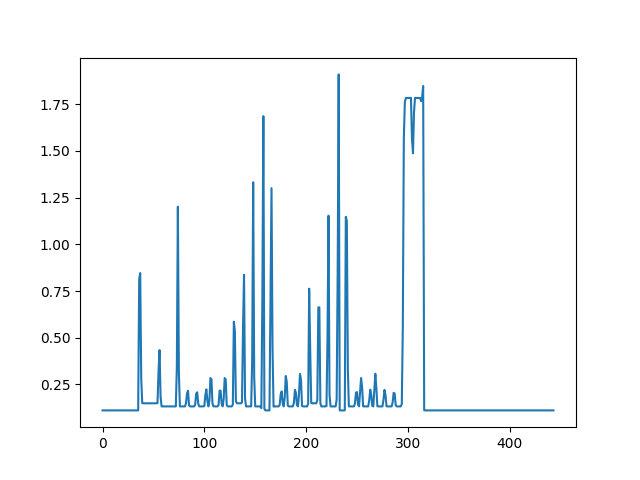
얼추 k-평균과 비슷하게 결과가 나온다. 통상적인 인공신경망의 훈련에서 이뤄지는 일을 생각하면 결과가 비슷한 게 당연하다.
역시나 단순한 문제에는 ANN이 굳이 필요치 않다. 하지만 블로그 제목을 생각하면 어떻게든 신경망을 써야 할 것 같다. k-평균으로 해결이 어렵지만 ANN으로는 가능한 문제가 있을까?
