배경 소음 줄이기
한 줄 요약: 배경 소음을 제거하는 방법을 몇 가지 시도해 봤는데 ANN 방식이 개중 낫지만 만족스러운 정도는 아니다.
4분 55초짜리 공장 소리 영상이 있다. 시끄러운 와중에 몇 가지 소리가 섞여서 들린다.
import numpy as np
import librosa
import librosa.display
import matplotlib.pyplot as plt
y, sr = librosa.load('factory.mp3')
ft = librosa.stft(y)
db = librosa.amplitude_to_db(np.abs(ft), ref=np.max)
librosa.display.specshow(db, x_axis='time', y_axis='linear')
plt.show()
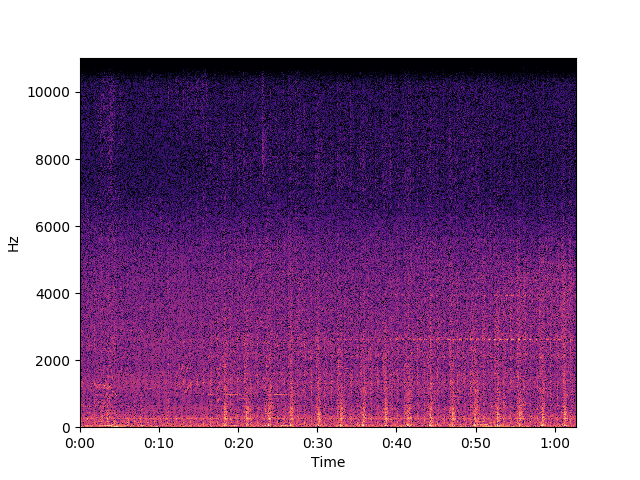
배경 소음은 크게 두 패턴이다. 앞쪽(0:0-1:44)에선 백색 잡음 같은 소리에 더해서 뭔가 두드리는 소리가 반복해서 들린다.
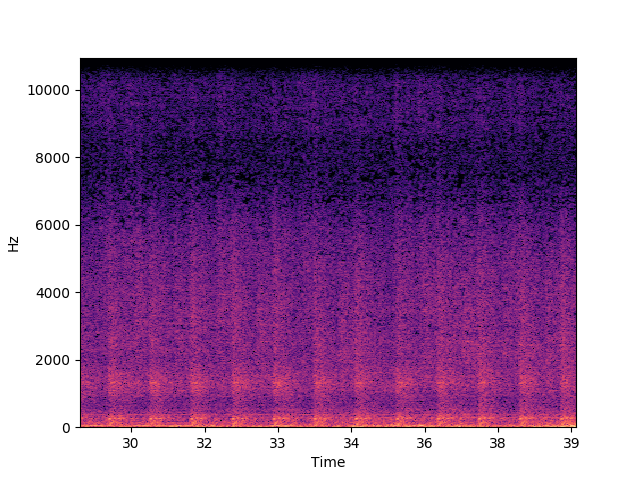
그후로는 거기 더해서 2~3초 주기의 좀 더 크고 낮은 충돌 소리가 들린다.
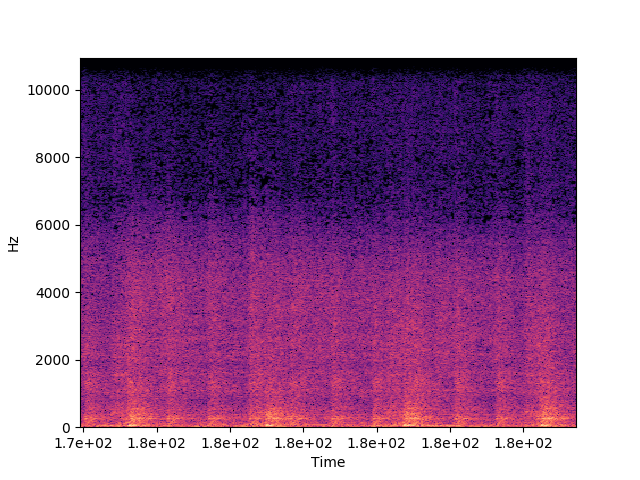
그리고 4:25 시점에 다시 이전 패턴으로 돌아간다. 요컨데 최소 세 가지 소리가 섞여서 배경 소음을 이룬다.
그 속에서 다음 소리가 들린다.
- 부우웅: 0:2-0:10
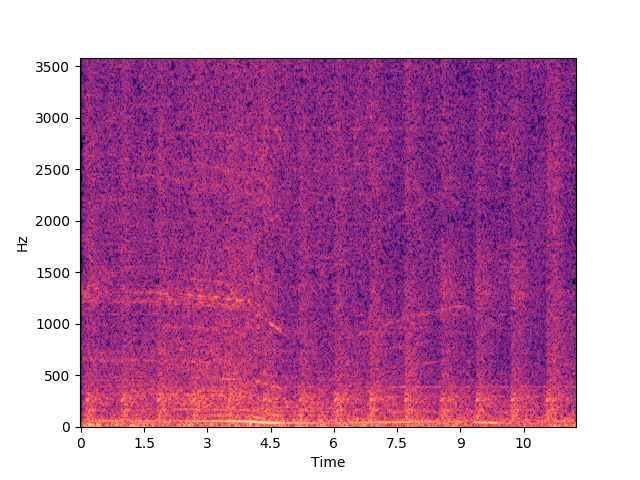
- 애애앵: 0:26-0:28, 0:40-0:42, 2:10-2:12, 2:20-2:22
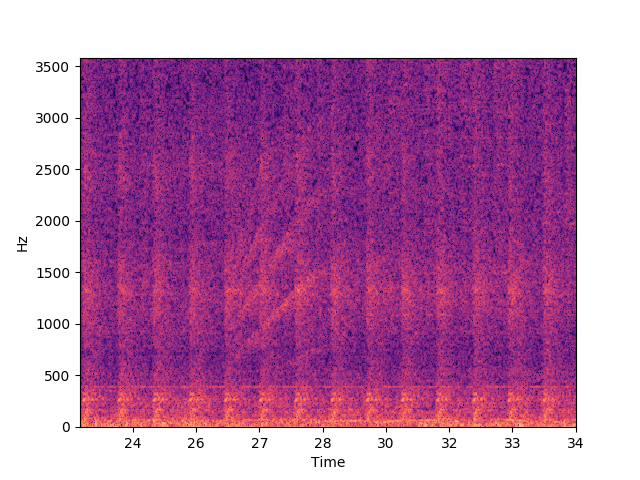
- 딩동댕동: 2:13-2:48
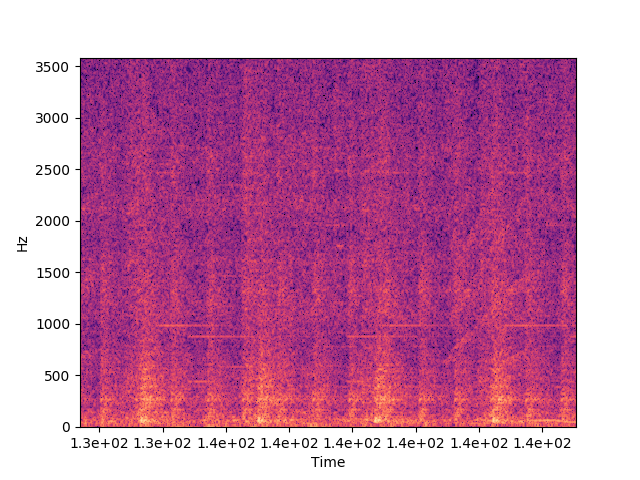
- 삑삑삑삑: 3:52-4:13
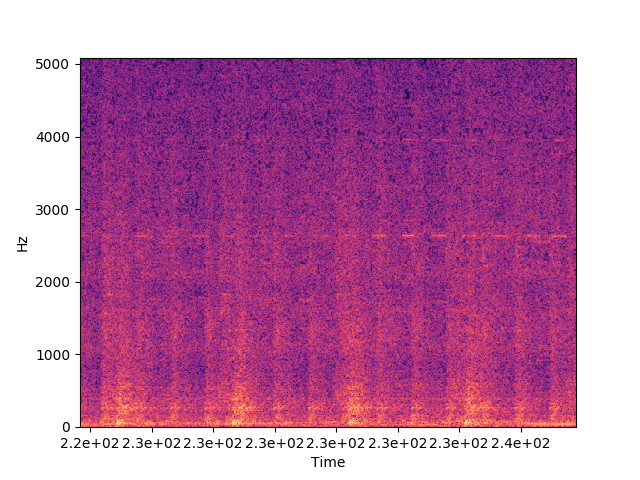
꽤 분명하게 패턴이 보인다. 근데 스펙트럼을 자세히 들여다보면 많이 울퉁불퉁하다.
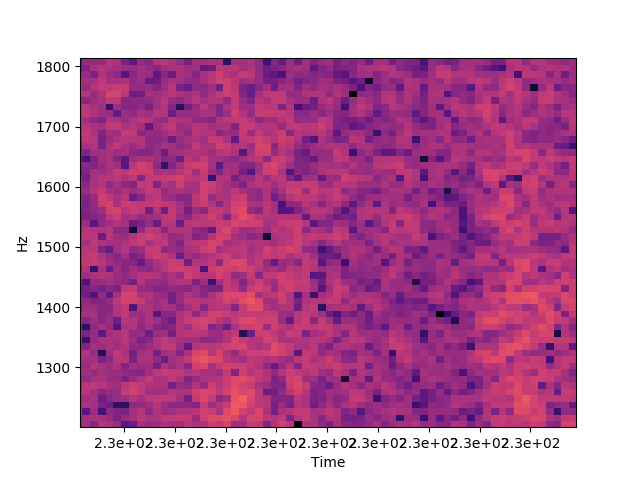
배경 소음을 제거해서 네 가지 소리가 더 잘 들리게 만들 수 있을까? 이왕이면 준실시간 처리가 가능한 방식으로, 또 이왕이면 범용적인 방식으로 말이다.
준실시간 처리가 가능한 방식이란 건 특정 시간 구간(프레임)의 데이터를 처리하는 데 과거 및 미래의 데이터를 한정된 범위로만 이용한다는 얘기다. 비교적 따르기 쉽다. 반면 범용성은 기본적으로 도달할 수 없는 목표다. 제거할 소리와 보존할 소리를 나눌 일반적 기준이 없기 때문이다.
일단 전체 소리를 배경 소음만 있는 구간과 듣고 싶은 소리까지 포함된 구간으로 나누자.
bg = np.c_[ft[:,500:1100], ft[:,1300:1700], ft[:,1850:5550],
ft[:,7250:9000], ft[:,11200:]]
fg = np.c_[ft[:,0:500], ft[:,1100:1300], ft[:,6000:6500],
ft[:,9500:11000]]
y = librosa.istft(fg)
librosa.output.write_wav('factory-fg.wav', y, sr)
fg가 나타내는 소리가 아래의 시도 결과들과 비교할 기준이다.
단순한 방식들: 별로
없애려는 소리의 주파수와 들으려는 소리의 주파수가 명확히 구별된다면 대역 필터만으로 충분할 수 있다. 이번 경우는 전혀 해당이 안 되지만, 그래도 한번 저대역과 고대역을 확 줄여 보자.
fg_bf = np.copy(fg)
fg_bf[:50] /= 100
fg_bf[400:] /= 100
y = librosa.istft(fg_bf)
librosa.output.write_wav('factory-bf.wav', y, sr)
db = librosa.amplitude_to_db(np.abs(fg_bf), ref=np.max)
librosa.display.specshow(db, x_axis='time', y_axis='linear')
plt.show()
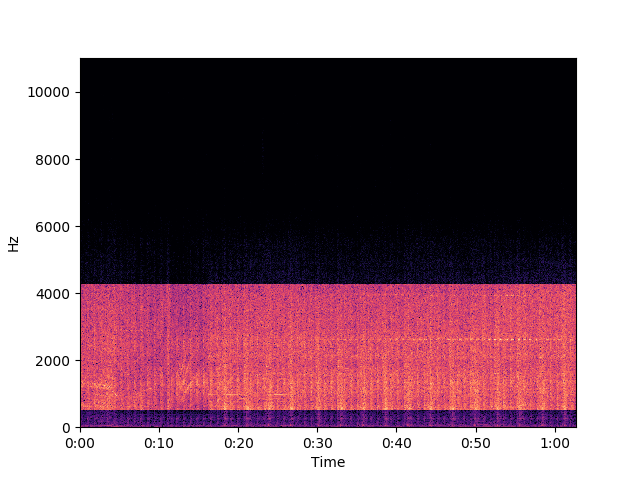
소리를 들어 보면 낮은 소리가 사라진 게 눈에 (아니, 귀에) 띄긴 하지만 쿵쿵 두드리는 소리가 여전하다. 그리고 사람의 개입(대역 결정)이 필요하므로 범용성이 떨어진다.
배경 소음이 일정한 편이라면 (예: 서버실) 그 평균치를 구해서 빼 볼 수 있다. 마찬가지로 이번 경우는 해당이 안 되지만 그래도 한번 해 보자.
bg_avg = np.mean(np.abs(bg), axis=1)
plt.plot(bg_avg)
plt.show()
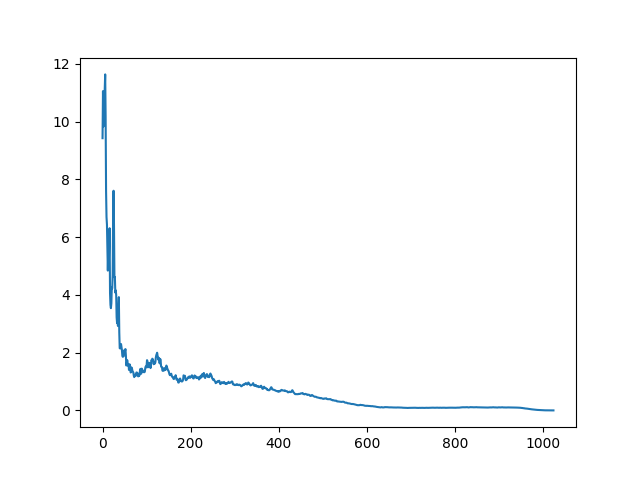
저음 성분 진폭이 아주 큰 게 눈에 띈다. 모든 프레임에서 이 패턴을 빼 보자.
bg_avg = np.repeat(bg_avg, len(fg[0])).reshape((len(fg), len(fg[0])))
fg_diff = (np.abs(fg) - bg_avg) * (fg / np.abs(fg))
y = librosa.istft(fg_diff)
librosa.output.write_wav('factory-diff.wav', y, sr)
db = librosa.amplitude_to_db(np.abs(fg_diff), ref=np.max)
librosa.display.specshow(db, x_axis='time', y_axis='linear')
plt.show()
스펙트럼이 전체적으로 좀 어두워지고 들으려는 소리들이 좀 뚜렷해진 같다. 들어 보면 배경 소음이 꽤 많이 사라졌지만 (당연하게도) 쿵쿵거리는 소리가 선명하게 남아 있다.
없애고 싶은 소리를 역으로 더한다는 점에서 일종의 능동 소음 제어인 셈인데, 여기서 문제의 핵심은 제거할 소리를 어떻게 식별해 낼 것인가이다.
k-평균: 시망
k-평균을 이용해 볼 수 있을까? 배경 소음이 반복되니까 프레임들을 비슷한 것끼리 분류할 수 있을 거다. 그러고서 입력이 들어오면 가장 비슷한 배경 소음 패턴을 찾고, 입력에서 그 패턴을 빼면 듣고 싶은 소리가 나올 거다. 깔끔하다.
사소한 문제라면 비슷한 배경 소음 패턴을 찾는 게 잘 안 된다는 점이다. 뭔가 들을 게 있는 프레임이라면 기존 패턴들에는 없는 성분 값이 있을 것이고, 그게 탐색을 방해한다. (k-평균 알고리듬은 유클리드 거리를 이용하기 때문에 튀는 값에 영향을 많이 받는다.) ANN을 비슷한 방식으로 이용하려 할 때도 마찬가지 문제가 발생한다.
그렇다면 전체 대역을 통째로 다룰 게 아니라 여러 작은 구간들로 나눠서 처리하면 어떨까? 입력이 들어오면 각 대역별로 가장 비슷한 배경 소음 패턴을 찾아 보고, 그 패턴과의 거리가 일정 이하면 그 대역을 0으로 채우고 (즉 익숙한 배경 소음을 제거하고) 아니면 입력의 값을 유지하는 거다. 요컨데 유지할 소리 성분을 찾아내는 거다.
사람의 실제 감각에 가깝도록 진폭을 로그 스케일로 바꿔서 처리하자. 그리고 너무 작은 소리는 무시하자. 기준 거리는 평균 거리의 1.5배로 잡아 보자.
from scipy.cluster.vq import kmeans2
intervals = []
for start, end, step in [(0, 425, 5), (425, 1025, 10)]:
for i in range(start, end, step):
intervals.append((i, i+step))
dist_mean = {}
centroid_set = {}
for l, r in intervals:
band = np.transpose(np.clip(np.log10(np.abs(bg[l:r])+1e-10), -4, None))
centroid, label = kmeans2(band, 108)
dist = [np.linalg.norm(p - centroid[label[i]]) for i, p in enumerate(band)]
dist_mean[l] = np.mean(dist)
centroid_set[l] = centroid
어떤가 보자.
def to_cluster(p, centroids):
dist = map(lambda c: np.linalg.norm(p - c), centroids)
return min(enumerate(dist), key=lambda e: e[1])
def intervalwise_reduce(ft, thre):
res = np.empty(np.shape(ft), dtype=np.complex)
for l, r in intervals:
band = np.clip(np.log10(np.abs(ft[l:r])+1e-10), -4, None)
_, dist = to_cluster(band, centroid_set[l])
if dist < thre * dist_mean[l]:
res[l:r] = 0
else:
res[l:r] = ft[l:r]
return res
fg_t = np.transpose(fg)
fg_kmeans = np.transpose(np.array([intervalwise_reduce(f, 1.5) for f in fg_t]))
y = librosa.istft(fg_kmeans)
librosa.output.write_wav('factory-kmeans.wav', y, sr)
db = librosa.amplitude_to_db(np.abs(fg_kmeans), ref=np.max)
librosa.display.specshow(db, x_axis='time', y_axis='linear')
plt.show()
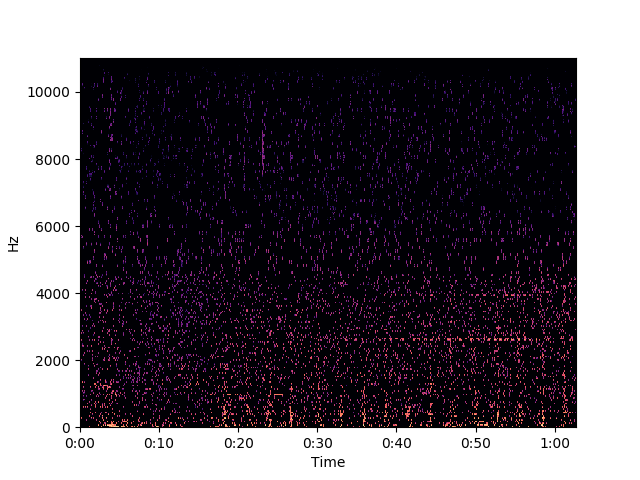
공장 소음을 없애려다 SF 소음을 얻었다. 스펙트럼을 자세히 살펴보면 원하는 소리를 얼추 뽑아내기는 했다.
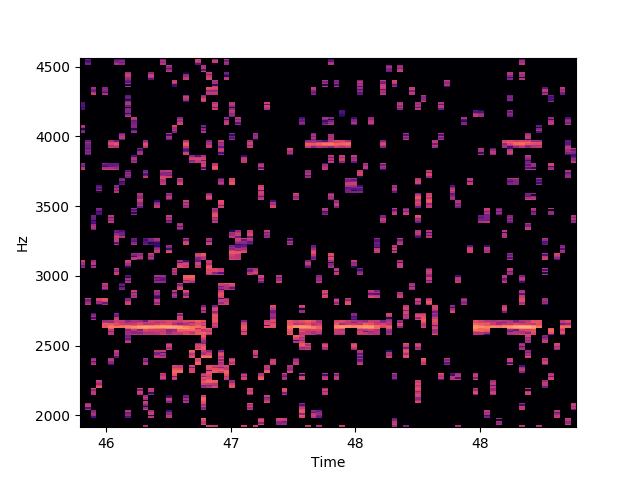
문제는 다른 잡다한 소리들까지 뽑아냈다는 거다. 결론은 실패. 설령 기능적으로 괜찮더라도 성능이 구리니 어쨌든 실패.
ANN: 애매
앞선 시도에선 한 프레임을 여러 대역들로 나눠서 각각을 따로 다뤘다. 하지만 성분들이 서로 연관된 경우도 많다. 지금 다루는 소리가 특히 그런데, 쿵쿵거리는 소리가 날 때 전체 대역의 진폭이 함께 커진다.
성분들 사이에 연관성이 있다면 어떤 대역을 입력으로 해서 다른 대역의 값을 추측하도록 신경망을 훈련시키는 게 가능하다. 들으려는 소리가 특정 주파수 범위 내에 있고 그 범위를 미리 알 수 있다면 나머지 대역의 값을 입력으로 줘서 그 범위의 값을 추측해 볼 수 있다. 그러고서 입력과의 차이를 구하면 된다. 200~5400Hz 정도 대역을 채우도록 망을 훈련시켜 보자.
import keras
bg_t = np.transpose(np.abs(bg))
bg_t_in = np.copy(bg_t)
bg_t_in[:,20:500] = 0
bg_t_out = np.copy(bg_t)
data_size = len(bg_t[0])
layer_0_1 = keras.layers.Input(shape=(data_size,))
layer_1_1 = keras.layers.Dense(500, activation='relu')(layer_0_1)
layer_1_2 = keras.layers.Dropout(0.1)(layer_1_1)
layer_2_1 = keras.layers.Dense(500, activation='sigmoid')(layer_1_2)
layer_2_2 = keras.layers.Dropout(0.1)(layer_2_1)
layer_0_and_2 = keras.layers.Concatenate()([layer_0_1, layer_2_2])
layer_3_1 = keras.layers.Dense(500, activation='sigmoid')(layer_0_and_2)
layer_1_and_3 = keras.layers.Concatenate()([layer_1_2, layer_3_1])
layer_4_1 = keras.layers.Dense(500, activation='relu')(layer_1_and_3)
layer_2_and_4 = keras.layers.Concatenate()([layer_2_2, layer_4_1])
layer_5_1 = keras.layers.Dense(500, activation='relu')(layer_2_and_4)
layer_3_and_5 = keras.layers.Concatenate()([layer_3_1, layer_5_1])
layer_6_1 = keras.layers.Dense(500, activation='sigmoid')(layer_3_and_5)
layer_4_and_6 = keras.layers.Concatenate()([layer_4_1, layer_6_1])
layer_7_1 = keras.layers.Dense(500, activation='relu')(layer_4_and_6)
layer_5_and_7 = keras.layers.Concatenate()([layer_5_1, layer_7_1])
layer_8_1 = keras.layers.Dense(data_size, activation='relu')(layer_5_and_7)
filler = keras.models.Model(layer_0_1, layer_8_1)
filler.compile(optimizer='rmsprop', loss='logcosh')
filler.fit(bg_t_in, bg_t_out,
epochs=5000, batch_size=100,
shuffle=True, verbose=0,
validation_data=(bg_t_in, bg_t_out))
fg_t = np.transpose(np.abs(fg))
fg_t_in = np.copy(fg_t)
fg_t_in[:,20:500] = 0
fg_ann_pred = np.transpose(filler.predict(fg_t_in))
fg_ann = (np.abs(fg) - fg_ann_pred) * (fg / np.abs(fg))
y = librosa.istft(fg_ann)
librosa.output.write_wav('factory-ann.wav', y, sr)
db = librosa.amplitude_to_db(np.abs(fg_ann), ref=np.max)
librosa.display.specshow(db, x_axis='time', y_axis='linear')
plt.show()
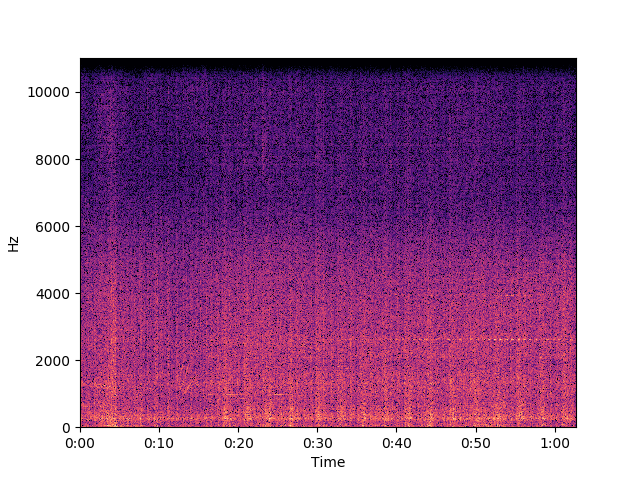
들어 보면 두드리는 소리가 꽤 줄어서 지금까지 결과들 중엔 가장 낫다. 하지만 여전히 만족스런 수준은 아니다.
이 방식은 앞서 언급한 것처럼 들을 소리가 포함된 대역이 정해져 있어야 한다는 제약이 있고, 그래서 범용성에 한계가 있다. 대안으로 다음 방식을 생각해 볼 수 있다.
- 대역 A를 A1, A2, A3로 나눈다.
- A1 값을 입력받아서 A 값을 출력하는 망 N1을 훈련시킨다. 비슷하게 A2와 A3를 입력으로 하는 망 N2와 N3를 훈련시킨다.
- 대역 A 값을 입력받아서 A1, A2, A3로 나눠서 N1, N2, N3에 각각 입력한다.
- 세 가지 출력 중 서로 비슷한 둘을 (평균을 내거나 해서) 배경 패턴으로 채택한다.
이렇게 하면 들을 소리가 A1, A2, A3 중 최대 한 곳에만 등장한다는 전제 하에 더 정확한 배경 패턴을 기대할 수 있다. 근데 간단히 해 보니 늘어나는 복잡도에 비해 결과가 딱히 좋은 것 같지는 않다.
단순하게 차이를 구하는(np.abs(fg) - fg_ann_pred) 대신 좀 더 섬세한 처리를 하면 소리를 더 뚜렷하게 만들 수 있을지 모른다. 하지만 직접 해 보긴 귀찮으니 패스.
또 한편으로, 스펙트럼 그래프를 살펴보면 들으려는 음에 해당하는 형태가 보인다. 즉 유의미한 소리를 찾는다는 건 x축이 시간이고 y축이 주파수인 2차원 그레이스케일 이미지에서 익숙한 패턴(폭이 비교적 좁은 수평선이나 사선 등)을 찾아서 강조하고 나머지 성분은 제거하는 작업으로 생각할 수도 있다. 이건 나중 언제 기회 되면…
주목(attention): 실패
사람은 ‘귀를 기울일’ 수 있다. 즉 특정 성분에 주목할 수 있고, 그러면 나머지 소리는 감쇄되고 그 성분은 또렷하게 들린다. 이걸 어떻게 흉내낼 수 있을까?
일단 사람 청각의 넓은 다이나믹 레인지를 생각하면 로그 스케일이 실제 감각에 더 가까울 거다.
fg_att = np.log10(np.abs(fg) + 1e-10)
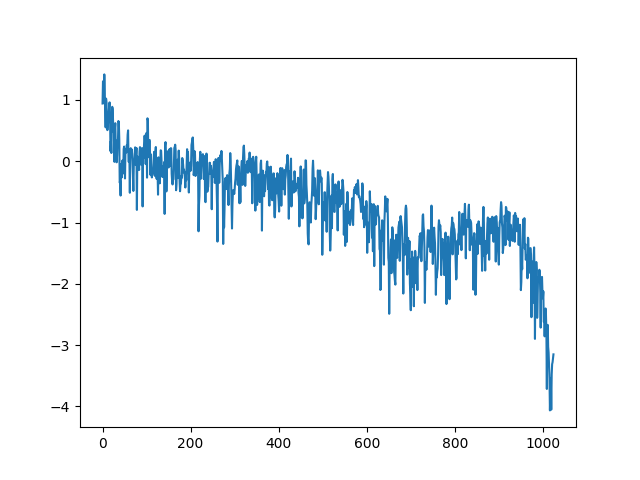
앞서도 봤지만 저주파 대역 진폭이 크다. 근데 실제 소리를 들어 보면 저음이 그렇게 크게 들리진 않는다. 사람의 귀가 모든 주파수를 같은 민감도로 인식하진 않기 때문이다. 등청감 곡선을 이용해 정규화를 해 보자.
import pydsm
spl_itpl = pydsm.iso226.iso226_spl_itpl(L_N=60)
elc = np.array([spl_itpl(i*sr/2048) for i in range(len(fg_att))])
fg_att = np.transpose(np.transpose(fg_att) - (elc - 60)/20 + 1)
fg_att[0] = 0
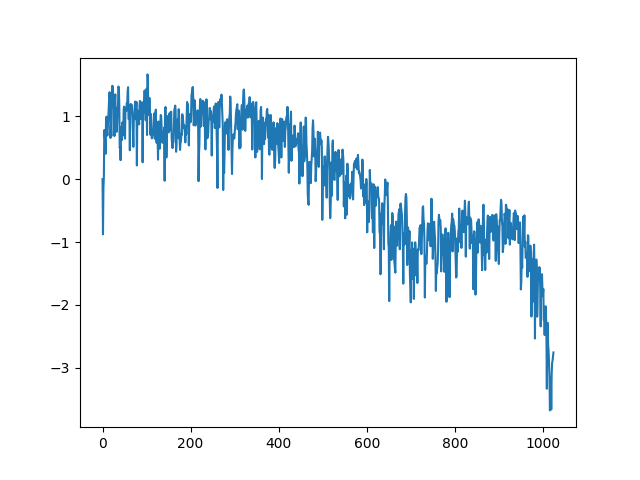
거시적인 모양새는 맘에 드는데 미시적으로 보면 너무 뾰족거린다. 이동 평균을 구해서 좀 부드럽게 만들어 보자. 하는 김에 두 가지 범위로 구해 보자.
fg_att_t = np.transpose(fg_att)
fg_att_ma_n = np.array([np.convolve(np.r_[f[1:4:1],f,f[-2:-5:-1]], np.ones(7)/7, 'valid') for f in fg_att_t])
fg_att_ma_w = np.array([np.convolve(np.r_[f[1:12:1],f,f[-2:-13:-1]], np.ones(23)/23, 'valid') for f in fg_att_t])
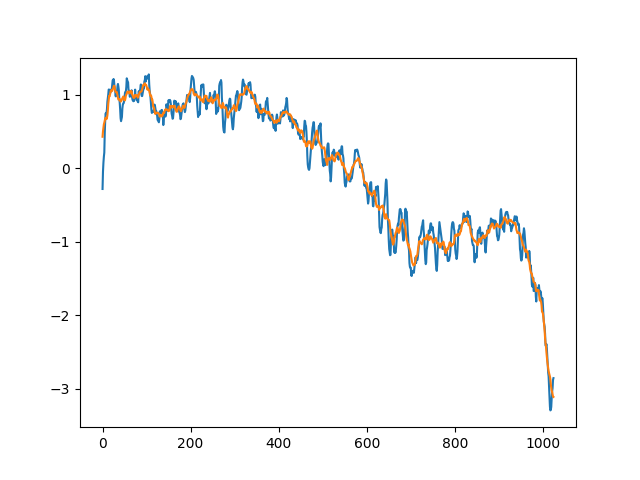
좁은 범위 이동 평균(fg_att_ma_n)에서 넓은 범위 이동 평균(fg_att_ma_w)을 뺀 값이 크면 ‘신경이 쓰이게’ 된다. 또 소리 자체가 커도 신경이 쓰인다.
fg_att_sum = np.clip(np.clip(fg_att_t, 0, None) * (fg_att_ma_n - fg_att_ma_w), 0, None)
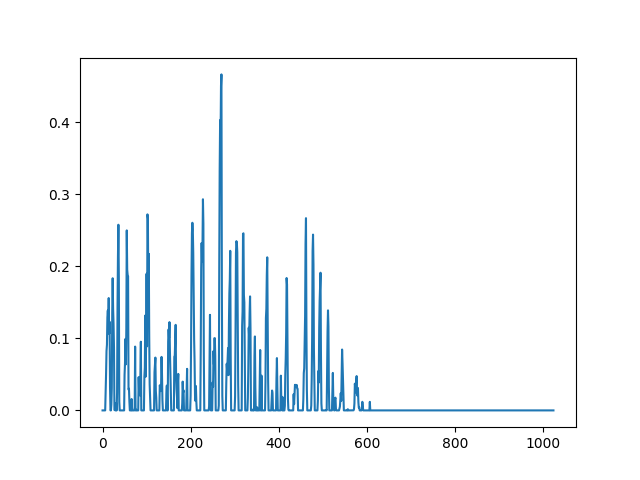
비슷한 소리가 계속 들리면 주의를 집중하고 안 들리면 귀를 기울이지 않게 된다. 그리고 어떤 소리가 들리면 인접 주파수에도 신경이 쓰이게 되…ㄹ지도 모른다.
fg_att_timed = np.empty(np.shape(fg_att_sum))
att = np.zeros(len(fg_att_sum[0]))
for i, f in enumerate(fg_att_sum):
att = np.clip(att - (1. - att/3), 0, None)
att += f
l = np.roll(f, -1)
l[0] = 0
att += .8 * l
r = np.roll(f, 1)
r[0] = 0
att += .8 * r
att = np.clip(att, None, 2.)
fg_att_timed[i] = att
fg_att_final = np.transpose(10 ** (fg_att_timed - 1))
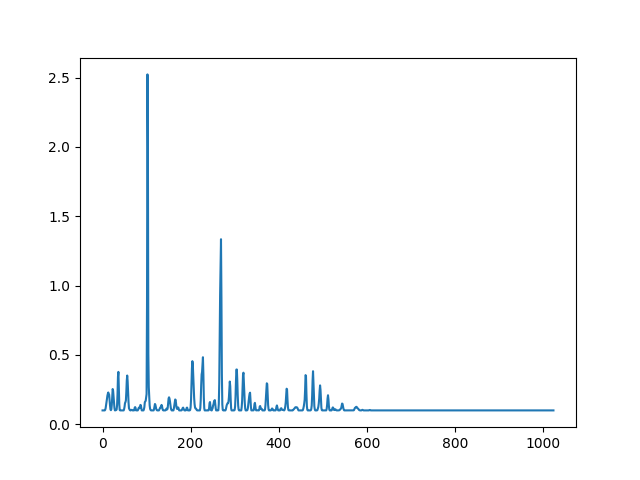
fg_with_att = fg_att_final * (fg / (np.abs(fg) + 1e-10))
y = librosa.istft(fg_with_att)
librosa.output.write_wav('factory-att.wav', y, sr)
db = librosa.amplitude_to_db(np.abs(fg_with_att), ref=np.max)
librosa.display.specshow(db, x_axis='time', y_axis='linear')
plt.show()
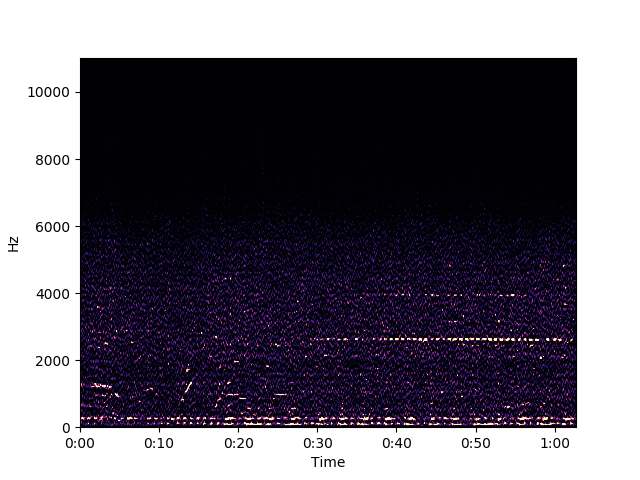
스펙트럼 모양새는 그럴듯한데 또 SF 소음이다. k-평균보다는 좀 낫지만 등청감곡선까지 등장시켜서 얻은 결과라기엔 아쉽다.
갖다 쓰기: 헛다리
rnnoise 라이브러리가 RNN을 이용해 잡음을 줄여 준다고 한다. 공장 소음도 줄여 줄까?
$ ffmpeg -i factory.wav -f s16le -ar 48k -acodec pcm_s16le factory.raw
$ rnnoise_demo factory.raw factory-rnnoised.raw
$ ffmpeg -f s16le -ar 48k -ac 1 -i factory-rnnoised.raw factory-rnnoised.wav
들어 보니 잡음이 거의 사라지긴 했는데 선명하게 남은 게 두드리는 소리다. 보아하니 음성 통화에서 잡음을 제거해서 사람 목소리를 선명하게 만들도록 RNN을 훈련시키고서 그 결과를 라이브러리 형태로 만든 것 같은데, 공장 소리에는 적당치 않은 것 같다.
Krisp라는 잡음 제거 앱에서도 신경망을 이용하는 모양인데, 마찬가지로 사람 목소리가 대상이다.
2019-07-27:
능동 소음 제어 기술의 활용 분야로 이어폰/헤드폰 외에 가정(특히 부엌)이나 공장 등에서의 소음 제거도 있고, 제품도 꽤 나와 있다. 능동 소음 제어 기술로 층간 소음도 줄일 수 있을까? 검색해 보니 관련 특허도 나오는데 제품은 잘 안 보인다. 수요는 (특히 우리나라에선) 충분할 것 같은데, 팔릴 만한 형태로 만들긴 어려운 걸까?
